Khoảng cách là gì? Công thức tính khoảng cách đầy đủ và chính xác

Bài viết tổng hợp các công thức tính khoảng cách phổ biến trong hình học phẳng và hình học không gian chính xác và đầy đủ nhất, như: khoảng cách từ điểm tới điểm, từ điểm tới đường thẳng, từ điểm tới mặt phẳng, giữa 2 mặt phẳng, giữa 2 đường thẳng chéo nhau,…

Khoảng cách và công thức tính khoảng cách

Khoảng cách là đại lượng để tính độ dài, độ rộng, độ cao của đoạn thẳng nối giữa hai điểm nào đó. Khác với vị trí trong các hệ tọa độ, khoảng cách là một đại lượng không có các giá trị âm. Khoảng cách là một đại lượng vô hướng, nó chỉ có độ lớn mà không có hướng như các đại lượng véc tơ.

Đơn vị đo độ lớn của khoảng cách trong khoa học được tính theo hệ đo lường quốc tế là mét và các bội số hay ước số của nó.

Khoảng cách là khái niệm được dùng phổ biến trong toán học và đặc biệt được dùng rất nhiều trong ngành xây dựng.

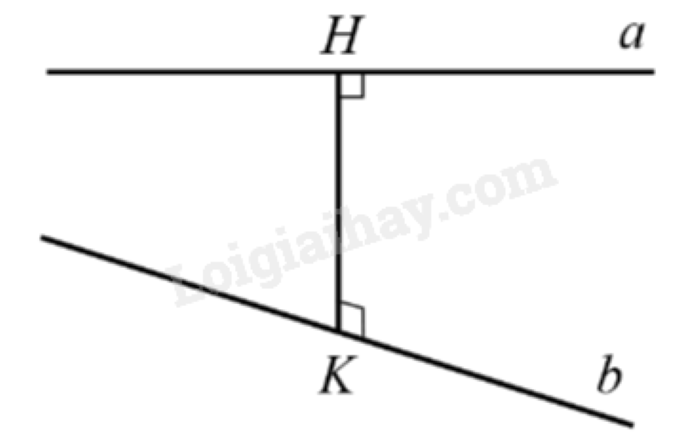
Khoảng cách là đại lượng được sử dụng phổ biến trong toán học

Các đơn vị đo khoảng cách thường dùng

Ở nước ngoài, người ta thường sử dụng các loại đơn vị đo chiều dài phổ biến như feet, yard, dặm. Tuy nhiên, tại Việt Nam, chúng ta thường sử dụng bảng đơn vị đo khoảng cách theo hệ m. Đây là các đơn vị đo chuẩn hệ SI được sử dụng trên toàn thế giới nói chung .Và cũng là hệ đo lường chính được sử dụng ở Việt Nam.

Đơn vị đo khoảng cách Kilomet

Kilomet là đơn vị đo độ dài ở những khoảng cách lớn, được ký hiệu là km. Chữ kilô (hoặc trong viết tắt là k) viết liền trước các đơn vị trong hệ đo lường SI, chỉ rằng đơn vị này được nhân lên 1000 lần.

Ở Việt Nam nó còn có tên gọi khác là cây số, 1 cây số =  1km. Vì thế nên ta thường gọi tốc độ chạy của xe máy là 50 cây số trên giờ.

* 1 km bằng bao nhiêu feet, inch, yard, hải lý?

1 km = 1.093,613 yard (yd).

1 km = 3.280,84 ft.

1 km = 39,37×103 in

1 km = 0,621 dặm Anh.

1 km = 0.539956803 hải lý

1 km = 546.806649 sải

* 1 km bằng bao nhiêu m, dm, cm, mm?

1 km = 1,0 × 10-6 gigamet( gm)

1 km = 0,001 megamet( mg)

1km = 1000m

1km = 10,000dm

1km = 100,000 cm

1 km = 1,000,000 mm

1 km = 1,000,000,000,000 nm

1 km = 105,7×10−15 năm ánh sáng( ly).

Đơn vị đo khoảng cách chiều dài trung bình mét

Có tên quốc tế là metre, tên tiếng Việt là mét, viết tắt là m. Đây là đơn vị phổ biến nhất được sử dụng trong hệ SI trên toàn thế giới.

1 m bằng bao nhiêu inch, feet, yard, dặm Anh?

1 m = 39,37 in

1 m = 3,281 ft.

1 m = 1,094 yd

1 m = 621,371×10−6 mi ( dặm Anh).

1 m = 0.000539956803 hải lý

1 m = 105,7×10−18 năm ánh sáng (ly)

1 m = 6,685×10−12 AU.

* 1 mét bằng bao nhiêu km, dm, cm, mm?

1 m = 0.001 km

1 m = 0.01 hm ( Héctômét)

1 m = 0,1 dam( Đề-ca-mét)

1m = 10 dm

1m = 100 cm

1m = 1000 mm.

1m = 1.000.000.000 nano mét

Đơn vị đo khoảng cách km, m, mm

Đơn vị đo khoảng cách chiều dài milimet

Đây là đơn vị đo khoảng cách ngắn, sử dụng cho nhiều sản phẩm có kích thước nhỏ. Ký hiệu là mm.

* 1 mm bằng bao nhiêu feet, inch, yard, dặm Anh?

1 mm = 39,3701×10−3 in

1 mm = 3,2808×10−3 ft

1 mm = 1,0936×10−3 yd

1 mm = 621,3712×10−9 mi (dặm Anh)

* 1 mm bằng bao nhiêu km, m, cm, dm?

1 mm = 1×10−6 km

1 mm = 1000 m

1 mm = 0,01 dm

1 mm = 0,1 cm

1 mm = 1000 micrometers

1 mm = 1.000.000 nm

Tổng hợp công thức tính khoảng cách thường dùng

1. Khoảng cách giữa hai điểm:

Trong mặt phẳng (2D): Cho hai điểm A(x₁, y₁) và B(x₂, y₂), khoảng cách giữa chúng là: d(A, B) = √((x₂ - x₁)² + (y₂ - y₁)²).

Trong không gian (3D): Cho hai điểm A(x₁, y₁, z₁) và B(x₂, y₂, z₂), khoảng cách giữa chúng là: d(A, B) = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²).

2. Khoảng cách từ một điểm đến một đường thẳng:

Trong mặt phẳng (2D): Cho đường thẳng d: Ax + By + C = 0 và điểm M(x₀, y₀), khoảng cách từ M đến d là: d(M, d) = |Ax₀ + By₀ + C| / √(A² + B²).

Trong không gian (3D): Cho đường thẳng Δ đi qua điểm M₀(x₀, y₀, z₀) và có vector chỉ phương u→(a, b, c), và điểm M(x, y, z), khoảng cách từ M đến Δ là: d(M, Δ) = |[M₀M→, u→]| / |u→|, trong đó [M₀M→, u→] là tích có hướng của hai vector.

3. Khoảng cách từ một điểm đến một mặt phẳng:

Trong không gian (3D): Cho mặt phẳng (P): Ax + By + Cz + D = 0 và điểm M(x₀, y₀, z₀), khoảng cách từ M đến (P) là: d(M, (P)) = |Ax₀ + By₀ + Cz₀ + D| / √(A² + B² + C²).

4. Khoảng cách giữa hai đường thẳng song song:

Trong mặt phẳng (2D) hoặc không gian (3D): Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm bất kỳ trên một đường thẳng đến đường thẳng còn lại.

5. Khoảng cách giữa hai đường thẳng chéo nhau:

Trong không gian (3D): Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó.

Lưu ý:

- Các công thức trên có thể được áp dụng cho nhiều dạng bài toán khác nhau.

- Việc lựa chọn công thức phù hợp phụ thuộc vào dạng bài toán và thông tin đã cho.

- Trong không gian, việc sử dụng vector và tích có hướng giúp việc tính toán khoảng cách trở nên dễ dàng hơn.

Các công thức tính khoảng cách được sử dụng phổ biến trong toán học, nghiên cứu và trong sản xuất, xây dựng, thiết kế,… Với những thông tin trên, hy vọng Tân Phát đã cung cấp cho các bạn kiến thức hữu ích để áp dụng trong cuộc sống.